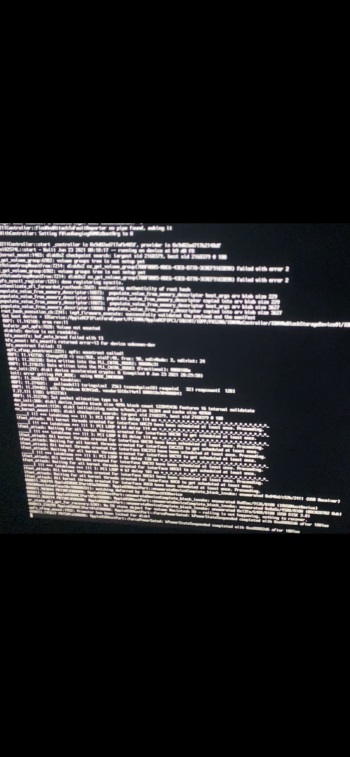
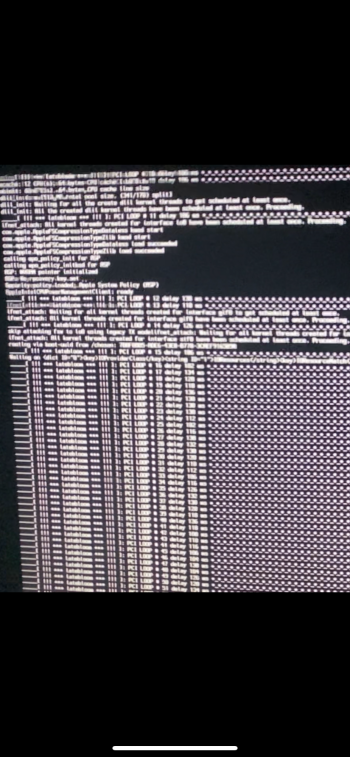
@Syncretic Wondering if the value for `lb_range` should always be added and never subtracted. Or is "sometimes less" also good against deadlocks?
For deadlocks, "more" or "less" aren't relevant, "random" is (at least when you're not in control of the whole system).
The classic example of a deadlock situation is the Dining Philosophers problem. Imagine a circular table with some number of seats. In front of each seat is a plate of spaghetti, and between each plate is a fork (thus there are the same number of forks as plates). Seated in each seat is a philosopher, who must eat some, then think for a while, then eat some more. In order to eat, a philosopher must have a fork in each hand, left and right - without two forks, the philosopher may not eat. A fork can only be used by one philosopher at a time.
If every philosopher at the table behaves by the same rules, each of them would reach to their right and pick up a fork, then look to their left and find no remaining forks, so none of them could eat - deadlock. If they then all lowered their right forks and picked up the one to their left, the same thing happens - no one can eat because none can get the necessary resources (two forks). What can they do to avoid starving?
They could choose to wait between attempts to pick up a fork - but again, if every one of them works by the same rules, they'd all wait the same amount of time and simultaneously repeat the one-fork pickup.
There are several possible solutions to this problem; many of them involve adding elements to the scenario or adding/changing the rules to adapt. A simple one is to introduce randomness - a philosopher will pick up either a left or right fork (randomly), then try to get the other fork; failing that, the philosopher will put down the fork and think for a random amount of time (presumably with some boundaries) before trying again. While this is not the most efficient system, it breaks the deadlock and allows the philosophers to eat. Because the delays are random, there are fewer cases where philosophers are "in sync," and when it does happen, they quickly get back out of sync.
In our case, it's unclear whether the random element is truly helpful, or just wishful thinking. While latebloom does mitigate the race condition for most systems, it's not addressing the underlying condition (it's an aspirin that eases the headache without affecting the brain tumor). If there is a deadlock happening, it's unclear whether or not it's directly related to the PCI bus probe, so randomly modulating the timing of those probes may or may not help with the deadlock. Assuming reasonable values are chosen, though, I don't think random values would have any negative effects. (In a nutshell, "it can't hurt.")
(My personal theory is that the real problem is in the APFS kext; however, manipulating that is far more difficult than this PCI hack, due to lack of both documentation and source code, plus the added risk of serious data corruption if there are any errors in the hack.)
Is anyone seeing different results (in terms of boot success/failure) between cold boot and warm reboot?
Right now it is only anecdotal but I have several hangs warm booting (rebooting) with 100 while success cold booting.
I haven't had time to do more of a "test" but was curious if anyone else noticed similar differences
From
post #1: "Note that while it's effective on either warm (restart) or cold (power-up) boots, testing shows it to be much more effective on cold boots, for reasons currently unknown. I welcome more test results to see if we can figure out why, and perhaps do something about it."